真理関数(しんりかんすう、英:Truth function) とは、数理論理学において、真理値の各変数の変域と終集合とがそれぞれ『「真な命題」と「偽な命題」のみから成る集合』に等しいような写像である。真理関数は命題関数でもある。
定義
真理関数を定義する為に次の 2 つの記号を用いる。
- 真な命題を表す記号 :
- 偽な命題を表す記号 :
L を と とだけから成る集合とし、n を自然数とする。そのとき、n 個の L の直積 から L への写像を n 変数の真理関数という。
主な真理関数
1 変数の真理関数 ¬ と 2 変数の真理関数 ∨、∧ とはそれぞれ以下の等式で定義される。ただし、A 、B は L の元の変数である。
¬A 、A∨B 、A∧B をそれぞれ、A の否定、A と B との論理和、A と B との論理積という。n 変数の真理関数は全部で 個ある。
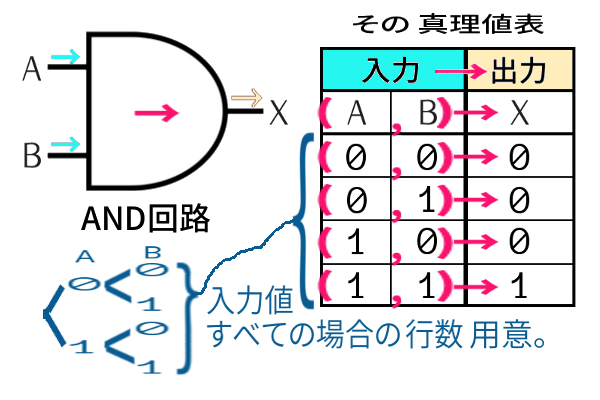
真理値表
真理関数の定義を真理値表という表を用いて示すことがある。
真理値表は次のように見る。¬ の真理値表の第 1 行は 「 A = であるとき、¬A = である 」 を意味する。∨ の真理値表の第 2 行は 「 A = 、B = であるとき、A∨B = である 」 を意味する。∧ の真理値表の第 3 行は 「 A = 、B = であるとき、A∧B = である 」 を意味する。
真理集合
F を n 変数の真理関数とするとき、F(X) = を満たす の元 X 全体から成る集合を F の真理集合といい、[F] で表わす。
例
2 つの真理関数 F と G とが等しいことは、F の真理集合と G の真理集合とが等しい為の必要十分条件である。
関連項目
- 数学基礎論、数理論理学、命題論理、ブール代数
- 否定、論理和、論理積、同値、否定論理積、真理値表
- 無矛盾律、排中律、交換法則、結合法則、分配法則、吸収法則、ド・モルガンの法則
- 命題関数、選言標準形、連言標準形
参考文献
- 前原昭二、復刊 数理論理学序説、共立出版株式会社、2010。